
But as as long as the previous solution $H^*$ remains feasible, the solution of the optimization problem does not change. Again, this amounts to adding constraints to the optimization problem and contracting its feasible set. In addition, one can add as many points as one wish to the data set without affecting $H^*$, as long as these points are well classified by $H^*$ and outside the margin. f sn m snchal m sngalais m spale m sparateur m sparation f spia. To see this, note that removing another point from the data set amounts to removing a non-active constraint from the quadratic program above. m hypermnsie f hyperplan m hyperplasie f hyperractivit f hyperralisme. These points (if considered with their labels) provide sufficient information to compute the optimal separating hyperplane. The support vectors are the data points $\g x_i$ that lie exactly on the margin boundary and thus that satisfy Īt this point, we formulated the determination of the optimal separating hyperplane as an optimization problem known as a convex quadratic program for which efficient solvers exist. Given a linearly separable data set $\ + b) \geq 1, \ i=1,\dots,N. You can click inside the plot to add points and see how the hyperplane changes (use the mouse wheel to change the label). The optimal separating hyperplane parameters : The support vectors are the highlighted points lying on the margin boundary. The plot below shows the optimal separating hyperplane and its margin for a data set in 2 dimensions. The resulting mesh can be plotted using existing methods in matplotlib. Afterwards, I derived the isosurface at distance 0 using the marching cubes implementation in scikit-image. Elaborating on this fact, one can actually add points to the data set without influencing the hyperplane, as long as these points lie outside of the margin. The solution is based on sampling the 3D space and computing a distance to the separating hyperplane for each sample. These points support the hyperplane in the sense that they contain all the required information to compute the hyperplane: removing other points does not change the optimal separating hyperplane. In particular, it gives rise to the so-called support vectors which are the data points lying on the margin boundary of the hyperplane. The optimal separating hyperplane is one of the core ideas behind the support vector machines. y ax + b is the equation of a line and is a very simple example of. For a three dimensional space, a line will be considered as a hyperplane.

Hyperplane is a subspace having one dimension less than the space under consideration. The optimal separating hyperplane should not be confused with the optimal classifier known as the Bayes classifier: the Bayes classifier is the best classifier for a given problem, independently of the available data but unattainable in practice, whereas the optimal separating hyperplane is only the best linear classifier one can produce given a particular data set. Aim of the SVM is to find the optimal hyperplane that is capable of separating the corresponding plane.
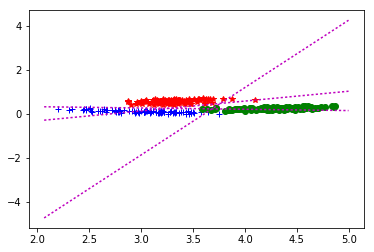
As a consequence, the larger the margin is, the less likely the points are to fall on the wrong side of the hyperplane.įinding the optimal separating hyperplane can be formulated as a convex quadratic programming problem, which can be solved with well-known techniques. Thus, if the separating hyperplane is far away from the data points, previously unseen test points will most likely fall far away from the hyperplane or in the margin.

New test points are drawn according to the same distribution as the training data. The idea behind the optimality of this classifier can be illustrated as follows. Il en rsulte aussi l'expression suivante du vecteur normal l'hyperplan sparateur : w xy 12.50 De l'quation 12.50, il dcoule que le vecteur.
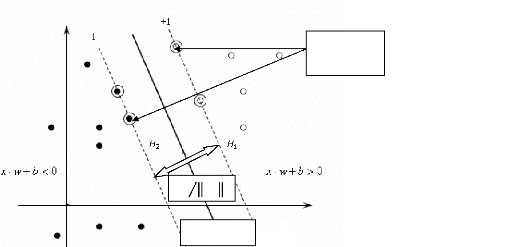
In this respect, it is said to be the hyperplane that maximizes the margin, defined as the distance from the hyperplane to the closest data point. In a binary classification problem, given a linearly separable data set, the optimal separating hyperplane is the one that correctly classifies all the data while being farthest away from the data points. Winter.The optimal separating hyperplane and the margin In words. Initially, huge wave of excitement ("Digital brains") (See The New Yorker December 1958) translation hyperplan séparateur from French into Russian by PROMT, grammar, pronunciation, transcription, translation examples, online translator and PROMT.Quiz: Given the theorem above, what can you say about the margin of a classifier (what is more desirable, a large margin or a small margin?) Can you characterize data sets for which the Perceptron algorithm will converge quickly? Draw an example.


 0 kommentar(er)
0 kommentar(er)
